Original English version: https://faculty.wcas.northwestern.edu/~infocom/The%20Website/pressure.html
| Materiell av press
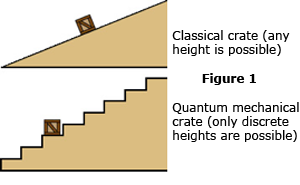
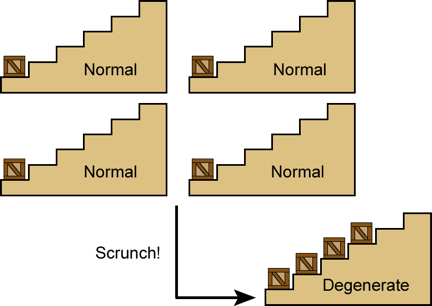
For å forstå stjernene, må du forstå press. Fra fødsel til død er det indre trykket til en stjerne skapt av egen vekt den mest dominerende faktoren i stjernens liv. Anta at du tar en haug med sand, og legger mer sand i den. Haugen vil bli større. Man kan forestille seg at dette også gjelder planeter eller stjerner, og det er det – men bare til et punkt. Saken er at det vi kaller “solid materie” er ikke noe av det på mikroskopiske skalaer. Materiale består av bittesmå atomer. Hvis du kunne utvide kjernen til et atom til størrelsen på en marmor, ville den veie tre milliarder tonn og den nærmeste kjernen ville ligge to mil unna. Mellom kjernene er det bare lette elektron “skyer”. (Se Tallerken 1 for mer informasjon om elektronisk sannsynlighetsskyer.) Milliarder tonn, halvtommers klinkekuler spredt miles fra hverandre tilsvarer mye tom plass, ikke fast stoff. Faktoren som gjør saken “solid” er den elektromagnetiske kraften som virker mellom atomene. Denne kraften, pluss reglene for kvantemekanikk, låser atomene i arrangementene som vi mennesker er glade for å kalle “solid”, mest fordi de kan motstå enhver kompresjonskraft som vår teknologi kan føre til. Men det er de ikke. Ingenting er solid hvis du bruker nok press på det. Ideen om at mer masse må være lik et større volum, gjelder bare for “små” objekter som planeten Jorden, hvis vekt ikke er nok til å komprimere kjernene deres for mye. (Selv for mindre planeter som Mars eller Jorden, er imidlertid det sentrale trykk fremdeles enormt. Jorden har et volum på omtrent 20% mindre enn man kan forvente at den ville ha, basert på dens kjemi, fordi dens vekt har komprimert det sentrale jernet. kjerne til omtrent det dobbelte av tettheten av jern som finnes på overflaten.) Når planeter blir mer massive, øker tendensen til gravitasjonskompresjon til slutt, med en masse som er omtrent 1,7 ganger den for Jupiter1 (540 jordmasser), når man et kritisk punkt der planeten slutter å bli større! Utover dette kritiske punktet2, legger mer masse til en planet faktisk den mindre fordi kompresjonen som er opprettet av den ekstra massen er større enn volumet av den ekstra massen. (Tallerken 2 har flere detaljer.) Fordi supermassive planeter kombinerer avtagende radius med økende masse, er densiteten (masse delt på volum) stratosfærisk, mange ganger bly. De sentrale temperaturer og trykk på supermassive planeter er så enorme at atomer ikke kan binde seg til hverandre, dvs. bergarter og is og andre forbindelser ikke kan eksistere. Alt du kan ha er individuelle atomer som svever rundt. Det er dermed mer nøyaktig å tenke på superplaneter som ekstremt tungt komprimerte kuler med gass, i stedet for som en flytende eller fast kjerne med en atmosfære pakket rundt seg. Kjernetrykk begrenser også hvor massiv en planet kan være: den veldig tette, blålige planeten illustrert i Tallerken 2 har en masse rett ved kanten av der du kan klemme på en ball med kald gass og fremdeles forvente at den skal oppføre seg som en kule kald gass. Øverst til venstre på platen illustrerer det fantastiske resultatet hvis du beveger deg utover dette, til rundt 75 Jupiter (24 000 jordmasser): hydrogensmelting antennes og “planeten” begynner å skinne! Den har blitt en dvergstjerne. Vi vil diskutere hva hydrogensmelting er, og hvordan det genererer store mengder kjernekraft, litt senere. Det viktige poenget her er at generering av varme dypt inne i planeten/stjernen transformerer den radikalt. Inerte superplaneter krymper bare mens du hoper på deg mer masse, men varmen i en stjerne øker trykket på gassene og stopper ytterligere sammentrekning. Faktisk fører den enorme energiproduksjonen fra større stjerner som vår sol til at de svulmer inn i enorme (om enn lette og dekket med flu) baller langt mer imponerende enn noen planet. (Se Tallerken 3 for mer informasjon om sola.) Solen og andre stjerner kan imidlertid opprettholde volumet bare så lenge de har en varmekilde for å generere høytrykksgass, og ingen varmekilde kan vare evig. Siden gravitasjonskomprimering er det vi er interessert i for øyeblikket, la oss pusse varmegenerering til side som bare en midlertidig veisperring og gå videre. Anta at vi har en 75 MJ planet/stjerne som ikke kan generere varme. Hva skjer i så fall når vi legger til mer masse? Det fortsetter selvfølgelig å krympe. For å gjøre en lang historie kort, massive gjenstander (uten varmekilde) slutter aldri å krympe når de blir mer massive. Men når de beveger seg inn i riket til 100 Jupiter-masser eller så, endrer de måten de krymper. Når atomene i en stjerne presses tettere sammen, når de til slutt et punkt der elektronskyene fra tilstøtende kjerner begynner å overlappe hverandre. Dette får stjernens fysikk til å ta en skarp sving inn i veldig merkelig territorium, fordi det betyr at kvantemekanikk nå kaller skuddene i stedet for klassisk fysikk. Det faktum at elektronene virkelig er skyer og ikke faste gjenstander (se Tallerken 1) kan føre til at du tror at det ville være enkelt å skvise sammen elektroner – og du vil ta ganske feil. Elektroner er kvantemekaniske skyer, ikke pust av luft, og som det skjer, avviser kvantemekanikk alvorlig av overlappende elektronskyer. (Denne avvisningen er teknisk kjent som Pauli-eksklusjonsprinsippet, etter fysiker Wolfgang Pauli.) Det er ikke lett å kondensere en diskusjon om kvantemekanisk teori i noen få avsnitt, men heldigvis trenger vi bare å dekke noen viktige punkter. Alt du trenger å vite om kvantemekanikken til stjerner Atomer er laget av protoner, nøytroner og elektroner. Protoner og nøytroner danner atomkjerner og er veldig tette, og veier inn til utrolige 1018 kg/m3. (Hvis hele jorden ble komprimert til proton/nøytrontettheter, ville den bare være rundt 700 fot på tvers.) Atomkjerner oppfører seg som veldig små, men veldig tunge partikler. Elektroner er en annen kjele med fisk. Langt mindre tette enn protoner eller nøytroner (med en faktor på 1013), sies elektroner vanligvis å “bane rundt” atomkjerner av populære forfattere, selv om de fleste av oss i fysikksamfunnet dumpet forestillingen om punkt-partikkelelektroner tilbake i 1927. Som utdypet i Tallerken 1, er ikke elektroner partikler som sådan. De er mer sammensatte enheter som fungerer som bølger mesteparten av tiden, men bærer likevel diskret masse og fart som om de er partikler. Nå kvantemekanikken kalles kvantemekanikk fordi elementærpartikler som elektronet er normalt begrenset til å okkupere energi og bevegelses stater (eller energinivå, hvis du vil) som eksisterer kun på bestemte kvantisert verdier. Bare elementære partikler som beveger seg fritt i verdensrommet og interagerer med ingenting, kan ta på seg hvilken som helst energi på samme måte som en bil på motorveien kan ta en hvilken som helst hastighet. For et elektron inne i et atom er de mulige energitilstandene den kan oppta, analoge med en kasseinnstilling på en trapp. (Se Figur 1 til høyre.) Kassen kan være på det ene trinnet, eller det neste, men det kan ikke hvile noe derimellom. I likhet med kassen kan et elektron spontant sprette “ned” trappen til en tilstand av lavere energi, men det kan aldri bevege seg “opp” trappen uten tilførsel av energi utenfra. I motsetning til kassen, vil imidlertid elektronet alltid bevege seg nedover før eller senere, med eller uten hjelp utenfra. Og veldig ulikt kassen, er det umulig å forutsi når elektronet kan gjøre dette: Alt du kan gjøre er å spesifisere en sannsynlighet for hvor lang tid det kan ta. (Hvis du ønsker å skyve kassen/trappene analogi til det ekstreme, kan du tenke deg en kasse med en opprørt kanin innelåst. Du vet at den vinglende kassen vil falle ned trappene til slutt, men du vet ikke når.) En annen måte et elektron skiller seg fra en kasse er at to kasser gjerne setter på samme trinn, men det er ikke to elektroner. Enkelt sagt kan to elektroner aldri okkupere den samme kvantetilstanden. De okkuperer ofte ofte den samme plassen, men det er annerledes. (Tenk deg to skyer med røyk fra forskjellige sigarer, og blander seg i luften. Det er det jeg mener når jeg sier at to elektroner kan “okkupere” det samme rommet. De kan begge ha en viss sannsynlighet for å være på samme punkt.) Hva elektronene kanskje ikke do er å okkupere det samme rommet og samtidig ha den samme energien og momentumet. Med andre ord, hvis skyer av sigarettrøyk virkelig oppførte seg som elektroner, ville røykskyer med samme temperatur og farge være nødvendig å sprette av hverandre som steiner i stedet for å blande! De kunne bare blandes hvis de hadde forskjellige temperaturer eller hadde forskjellige farger. Hvis dette virker litt rart – vel, sa jeg at det ikke var lett å forklare kvantemekanikk i noen få avsnitt. Hovedpoenget her er at elektronene overholder en eksklusjonsregel som forbyr dem å okkupere de samme kvante nivåene. Normalt gjelder imidlertid denne eksklusjonsregelen bare for elektroner som er innenfor samme atom. For “normal” sak (som den typen du er laget av), er elektronene festet til kjerner som er strødd over rommet i deg som så mange klinkekuler spredt miles fra hverandre. Det er god plass for den lille familien av elektronene i hvert atom til å ha den gunstigste – det vil si den laveste energien – tilstander alt for seg selv. (Se Tallerken 4 for en illustrasjon.) Dette lykkelige arrangementet tar slutt når elektronskyene begynner å overlappe i en kollapsende stjerne. I takt med at en økende prosentandel av dem knuses sammen, krever kvantemekanikkens regler at bare en av de billioner billionene trostiske elektronene i en kubikkcentimeter forblir i sin opprinnelige tilstand med lavest energi. Tenk på det som urbane boliger: hvis befolkningstettheten er lav nok, kan hver familie bo i et hus i ranchstil. Men når tettheten når den til Manhattan, så må noen leve 62 historier fra bakken. Elektroner er heller slik, bortsett fra verre. I kvanteversjonen av Manhattan er det bare ett elektron i hele byen som har lov til å bo i første etasje! De andre elektronene må skyves inn i høyere energitilstander, og siden det bare er en elektron per tilstand uansett hvor mange elektroner det er, svever elektronene raskt til forbløffende energier. I gjennomsnitt har elektronene i en kollapset stjerne 100 000 volt energi, noe som tilsvarer en “elektrontemperatur” godt over en milliard grader Kelvin3 hvis du tenker på elektronene som bare partiklene i en varm gass.4 (Det vil si at 100.000 volt er langt mer enn nok til å rive elektronene vekk fra individuelle kjerner, så elektronene står fritt til å vandre fra den ene siden av stjernen til den andre som en gass.) Saken sies av fysikere å ha kondensert inn i en ny og særegen tilstand som kalles elektron-degenerert materie. På dette tidspunktet har stjernen vår kanskje en kvart solmasse (omtrent 80 000 jordmasser), pakket i et volum som ikke er mer enn det dobbelte av jordens radius. Det er nå så tett at en flaske med elektron-degenerert materiale nær overflaten vil veie 50 tonn. Slike objekter er på ingen måte teoretiske: Melkeveis galaksen inneholder muligens ti milliarder av dem, og den første ble sett i 1862. Astronomer omtaler dem som hvite dverger, fordi de er veldig små og hvite varme. (Pride forplikter meg til å merke seg at teleskopet i Northwesterns Dearborn-observatorium var selve instrumentet som ble brukt for å gjøre det historiske 1862-synet! Ærlighet tvinger meg til å innrømme at Northwestern ikke skaffet seg teleskopet før i 1887; i 1862 var teleskopet fremdeles i Boston, hvor den ble produsert.) For normal materie – gass, væske eller faststoff – ser man for seg atomer som miniature solsystemer, med skyer av “planetariske” elektroner som omgir kjernefysiske “soler”. Noen få elektroner har lov til å oppføre seg som trillebiler og kan deles mellom nærliggende atomer for å danne kjemiske bindinger, men det er alt. For elektron-degenerert materie, som du kanskje forestiller deg, fungerer ikke dette “solsystemets” bildet. Elektronene i degenerert materie komprimeres så tett sammen at de mer eller mindre oppfører seg som om hele stjernen er et stort kvantesystem. De danner en elektrongass, og oppfører seg veldig som en væske med høyt trykk inne i stjernen. De elektron nakne kjernene oppfører seg mindre som “soler” og mer som blyskudd som glipper gjennom elektrongassen. Overraskende nok påvirkes kjernenes bevegelse nesten fullstendig av denne endringen i elektronisk entourage. De beveger seg fortsatt som om de er i en vanlig gass i stedet for en elektron-degenerert en. Det er to grunner til dette. For det første er ikke kjerner elektroner. Regler om at rasjonering elektronenergi er helt uten betydning for protonene5 og nøytronene 6 som utgjør kjerner. (Protoner og nøytroner har sine egne kvantetilstander, takk.) For det andre er kjernene mye tettere og mer massive enn elektronene. Når kjernene beveger seg, er de like glemte for energitilstandene til elektronene som en kanonkule er til atmosfærisk fuktighet. Hva dette betyr er, hvis du varmer eller kjøler elektron-degenerert materie, beveger kjernene seg raskere eller saktere akkurat som i en vanlig gass. Men i motsetning til en vanlig gass, bryr ikke elektronene seg og følger ikke etter. De er ikke knyttet til noen spesiell kjerne lenger, og faktisk, den eneste faktoren som har noen innvirkning på dem, er kampen for å skyve seg lenger fra hverandre og unngå utelukkelsesregelen. Den kampen er resultatet av den enorme kompresjonen som er skapt av den enorme tyngdekraften til den hvite dvergen, og tyngdekraften har ingenting med temperatur å gjøre. Dermed reagerer elektrongassen bare på endringer i massen av den hvite dvergen (dvs. for endringer i tyngdekraften), og ikke for endringer i temperaturen, noe som igjen betyr at en hvit dverg ikke endres i størrelse i det hele tatt når den varmes opp eller avkjøles. Det siste faktum er veldig kritisk, som vi skal se senere. Normale gasser endrer volumet når de blir oppvarmet eller avkjølt, og det er grunnen til at varm luft stiger og kjøligere gass faller. Men elektron-degenerert stoff oppfører seg mer som en eksotisk, fantastisk tett væske enn det gjør en gass, og væsker endrer ikke volumet mye når de varmes opp. De blir bare varmere. Derfor er elektron-degenerert materie mye vanskeligere å komprimere enn vanlig materie. (Det tar energi å løfte et elektron til et høyere nivå, og å heve alle elektronene i noe med massen til en stjerne tar mye energi.) Kort sagt, når det kommer til hvordan de reagerer på økt trykk eller temperatur, oppfører hvite dverger seg mer som “solide” kropper som jorden enn de gjør som gassformede kropper som Jupiter eller solen. Vi har nesten kommet full krets i diskusjonen vår om massive kropper. Nesten. I 1931 publiserte teoretisk astrofysiker Subrahmanyan Chandrasekhar (da bare 21 år gammel) en trio med oppsiktsvekkende artikler om elektronisk degenerert materie. Beregningene hans viste at når en hvit dverg blir mer massiv, må den uunngåelig nærme seg et kritisk punkt. Dette viser seg å være en konsekvens av Einsteins relativitetsteori, og siden jeg ikke kan forklare relativitet i et avsnitt, vil jeg bare skissere fakta: Når elektronene i en hvit dverg blir løftet til høyere energinivå, beveger de seg raskere. En av de mest grunnleggende relativitetslovene er at ingenting kan bevege seg raskere enn lysets hastighet (186.282 miles per sekund). Når partikler nærmer seg denne hastigheten, blir de umulige å akselerere fordi de begynner å få masse fra selve energien som presser dem! Dette er nedfelt i den berømte ligningen, E = mc2, som sier at energi kan omdannes til masse og omvendt. Omtrent sett får partikler nær lyshastighet masse fremfor energi, eller for å si det på en annen måte, de blir tyngre, men de går ikke raskere når du tilfører energi til dem. (Man kan ikke la være å tenke på et fett gris, fylle ned masse matenergi, men bli fetere og saktere i stedet for raskere og kraftigere.) Ved å bruke dette faktum, bemerket Chandrasekhar at elektrontrykket i en hvit dverg må ha en absolutt grense. Selv om den knuses til uendelig tetthet, vil hastighetsgrensen som ble pålagt av relativitet fremdeles tvinge en avskjæring til ethvert trykk de kunne utøve. Samtidig er det, alarmerende, ingen grenser for hvor mye masse du kan haffe deg på en hvit dverg. Verre er det at jo tyngre du gjør en, desto kraftigere blir gravitasjonskraften på overflaten. Isaac Newtons berømte lov om universell gravitasjon sier at tyngdekraften er proporsjonal med 1/r2, noe som betyr at hvis en planets radius krymper med en faktor av to, så må tyngdekraften på dens overflate stige med en faktor på fire. Chandrasekhar viste at det var et punkt der det ubegrensede fremskritt med økende masse og avtagende radius ikke lenger kunne opprettholdes. Som et strå som bryter en kamelrygg, vil det å tilføre mer hvit dverg på dette punktet føre til at dvergens gravitasjonskompresjon overskrider enhver mulig økning i elektrontrykket. Dermed ville dvergen krympe, men likevel sitte igjen med en enda verre gravitasjonsubalanse enn før. Den økte ubalansen ville få den til å krympe ytterligere og dermed forverre gravitasjonskrisen… Kort sagt, Chandrasekhar beregninger spådde at hvis en hvit dverg ble hevet utover en kritisk masse, ville den katastrofalt kollapse! Han beregnet denne kritiske massen til å være omtrent 1,4 ganger solens masse, og etter hvert ble den kjent som Chandrasekhar’s Limit. Det ville være rettferdig å si at denne nyheten fikk en svært blandet mottakelse i 1931. Kvantemekanikk var fremdeles et veldig ungt tema på den tiden (bare fire år gammel) og mange astrofysikere hadde fremdeles alvorlige tvil om hele teorien om kvantemekanikk, aldri husk troverdigheten til denne spesielle prediksjonen. Hvordan, spottet de, kunne en gjenstand halvparten så massiv som Solen og allerede komprimert til en nesten utenkelig tetthet, bare “kollapse”? Skjul til hva? Det var helt ubetydelig. Hvis Chandrasekhar ble tatt til sin logiske konklusjon, indikerte det at en hvit dverg som ble presset over grensen bokstavelig talt ville forsvinne – eller mer presist, ville den øyeblikkelig komprimeres til et uendelig punkt. Det manglet ikke astronomer som var skeptiske til denne ideen, for å si det mildt. Sir Arthur Eddington, den første astronomen som bekreftet Einsteins spådom om at Solens tyngdekraft kunne bøye stjernelys, og muligens den mest respekterte astronomen i sin tid, avfeide ganske enkelt spådommen ut av hånden. Det var faktisk i stor grad Eddingtons vokale kritikk av teorien som gjorde at den nesten ble ignorert i den bedre delen av et tiår. Og ennå, på dette tidspunktet hadde astronomer oppdaget dusinvis av hvite dvergstjerner… og ikke en hadde en masse over 1,4 solmasser, så langt det var mulig å bestemme. Det var noen få som følte at dette var for uhyggelig i samsvar med Chandrasekhar’s Limit for at hele ideen bare kunne bli avskjediget. Som vi skal se senere, viser hele historien om hva som skjer når en hvit dverg blir tatt utover 1,4 solmasser å være fantastisk og komplisert, men før vi kan fortelle den historien, må vi rette oppmerksomheten mot stjernefødsel, som vi vil gjøre i neste avsnitt. Før jeg fortsetter videre, vil jeg merke at Chandrasekhar forlot Cambridge for en fakultetsstilling ved Universitet av Chicago, der han ble lei av fiendtligheten til hans teorier fra Eddington og andre britiske astronomer, der han ble værende resten av livet. I 1983 ble han tildelt Nobelprisen i fysikk, først og fremst for sitt arbeid med hvite dverger. |
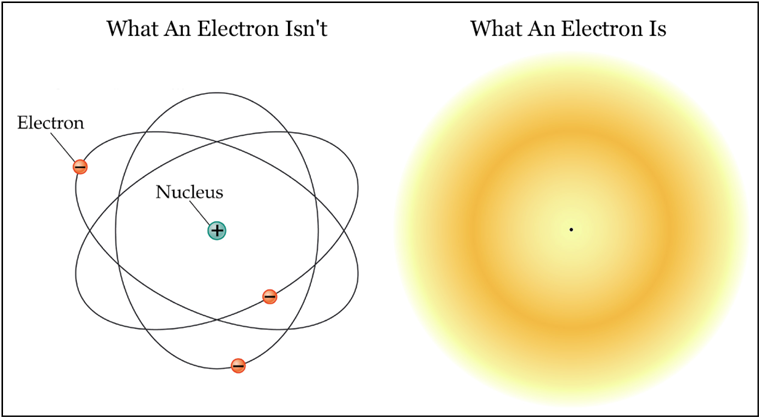 Tallerken 1 
Tallerken 2 1 – Jupiter er den femte planeten fra sola. Det er den mest massive gjenstanden i solsystemet bortsett fra solen selv, og faktisk, siden både Jupiter og solen nesten består av hydrogen og heliumgass, ligner Jupiter solen langt mer enn den gjør på jorden. Med ti ganger Jordens diameter og med en vekt på 318 jordmasser, er Jupiter 2,4 ganger mer massiv enn alle resten av planetene og månene i solsystemet til sammen. Forfatter Isaac Asimov sa en gang at “Solsystemet består av solen, Jupiter og litt rusk.” 2 – For puristene avhenger dette teoretiske maksimumet av flere antagelser, for eksempel om planeten består hovedsakelig av hydrogen og helium, eller ikke. For vårt formål er et estimat på 1,7 Jupiter-masser godt nok.
Tallerken 3
Notasjonen 1018 betyr bare at du har en etterfulgt av 18 nuller. Tilsvarende betyr 10–18 at du har et null, et desimalpunkt, deretter 17 nuller og et.
Tallerken 4 3 – Grader Kelvin er de samme som grader Celsius, bortsett fra at null C° tilsvarer frysepunktet for rent vann, mens null K° tilsvarer absolutt null, den kaldeste temperaturen som er mulig. Absolutt null er den teoretiske temperaturen der all bevegelse opphører, også atombevegelse. Kelvin-skalaen kalles derfor noen ganger også den absolutte temperaturskalaen. Absolutt null forekommer ved 0 K°, eller ved -459,69 F°, som du foretrekker. 4 – Varme er ganske enkelt tilfeldig bevegelse av små partikler. Jo mer energisk bevegelsen til de enkelte partiklene er, jo høyere er temperaturen for helheten.
5 – Protonet er positivt ladet og 1836 ganger mer massivt enn et elektron. Elektroner har samme ladning som protoner, bortsett fra med et negativt tegn, så antallet elektroner som omgir en kjerne, må være likt antall protoner. Delte elektroner lager kjemi, og dermed bestemmer protonnummeret til en kjern direkte kjemien. Hvert element i den periodiske tabellen tilsvarer en kjerne med et matchende protonnummer: element # 8 (oksygen) har åtte protoner, og så videre. 6 – Nøytroner har nesten nøyaktig samme masse som protoner (nøytroner er 0,06% mer massiv) men har ingen elektrisk ladning, derav navnet. Vanlig materiale består av omtrent 50% protoner og 50% nøytroner, så nøytroner som er låst inne i kjerner utgjør omtrent halvparten av normalstoffet i universet. I motsetning til protoner er frie nøytroner imidlertid ikke stabile. Utenfor kjernen forfaller nøytroner til et proton, et elektron og noe som kalles et anti-neutrino på omtrent 10,6 minutter. Frie nøytroner ble ikke oppdaget før i 1932.


|
David Taylor