Original English version: https://www.math.tamu.edu/~sottile/research/stories/MSRI04/index.html
Frank Sottile
9. oktober 2004, College Station, Texas.
Artikkel for høsten 2004 utgaven av Emissary, nyhetsbrevet til MSRI. ArXiv.org/math/0501146.
Denne artikkelen ble vist i Emissary, nyhetsbrevet til MSRI, og er oversatt til flere språk.
Alle vet at to punkter bestemmer en linje, og mange mennesker som har studert geometri vet at fem punkter på flyet bestemmer en kjegle. Generelt, hvis du har m tilfeldige punkter i flyet og ønsker å passere en rasjonell kurve av grad d gjennom dem alle, kan det ikke være noen løsning på dette interpolasjonsproblemet (hvis m er for stor), eller et uendelig antall løsninger (hvis m er for lite), eller et ubegrenset antall løsninger (hvis m er helt riktig). Det viser seg at “m akkurat passe” betyr m=3d-1 (m=2 for linjer og m=5 for kjegler).
En hardere spørsmål er, hvis m=3d-1, hvor mange rasjonelle kurver av graden d innskyte punktene? La oss kalle dette nummeret Nd, slik at N1=1 og N2=1 fordi linjen og konikken i forrige avsnitt er unike. Det har lenge vært kjent at N3=12, og i 1873 viste Zeuthen [Ze] at N4=620. Det var der saker sto til for omtrent ti år siden, da Kontsevich og Manin [KM] brukte assosiativitet i kvantekohomologi for å gi en elegant rekursjon for dette tallet.
Forskningstemaene i MSRI Winter 2004-semesteret om Topologiske aspekter av reell algebraisk geometri inkluderte enumerativ ekte algebraisk geometri, tropisk geometri, reelle plankurver og anvendelser av ekte algebraisk geometri. Alle er vevd sammen i den utfoldende historien om dette interpolasjonsproblemet, et prototypisk problem med enumerativ geometri, som er kunsten å telle geometriske figurer bestemt av gitte forekomstbetingelser. Her er et annet problem: hvor mange linjer i rommet møter fire gitte linjer? For å svare på dette, må du merke deg at tre linjer ligger på en unik dobbelt styrt hyperboloid.
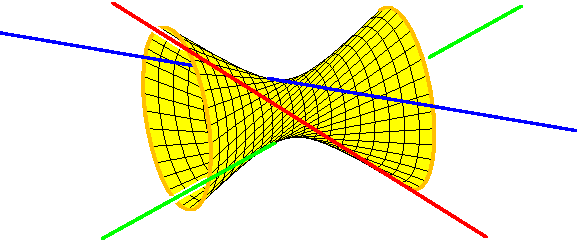
De tre linjene ligger i en kjennelse, og den andre kjennelsen består av linjene som møter de gitte tre linjene. Siden hyperboloiden er definert av en kvadratisk ligning, vil en fjerde linje møte den i to punkter. Gjennom hvert av disse to punktene er det en linje i den andre kjennelsen, og dette er de to linjene som møter våre fire gitte linjer.
Enumerativ geometri fungerer best over de komplekse tallene, da antallet reelle figurer avhenger ganske subtilt av konfigurasjonen av figurene som gir forekomstforholdene. For eksempel kan den fjerde linjen møte hyperboloiden i to virkelige punkter, eller i to komplekse konjugerte punkter, og det er derfor enten to eller ingen reelle linjer som møter alle fire. Basert på mange eksempler, har vi regnet med at alle tallrike problemer kan ha alle løsningene av dem [So].
Et annet slikt problem er de 12 rasjonelle kurvene som interpolerer 8 punkter i flyet. De fleste matematikere er kjent med nodal (rasjonell) kubikk vist til venstre nedenfor. Det er en annen type ekte rasjonell kubikk, vist til høyre.
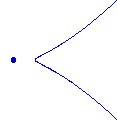
I den andre kurven møtes to komplekse konjugerte grener på det isolerte punktet. Hvis vi lar N(t) være antallet reelle kurver av type t som interpolerer 8 gitte poeng, så viste Kharlamov og Degtyarev [DK] at
N(
) – N(
) = 8 .
Her er en beskrivelse av sine elementære topologiske metoder.
Siden det er høyst 12 slike kurver, N() +N() \leq 12, og det er 8, 10 eller 12 reelle rasjonelle kubikk som interpolerer 8 reelle punkter i planet, avhengig av antall (0, 1 eller 2) kubikk med et isolert punkt. Dermed vil det være 12 reelle rasjonelle kubikker som interpolerer alle 8 av de 9 skjæringspunktene mellom de to kubikkene nedenfor.
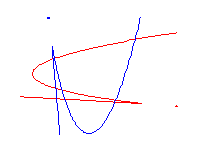
Welschinger [W], som var MSRI postdoc sist vinter, utviklet dette eksemplet til en teori. Generelt er singularitetene til en reell rasjonell plankurve C noder eller isolerte punkter. Pariteten til antall noder er dens sign s(C), som er enten 1 eller -1. Gitt 3d-1 reelle poeng i flyet, vurderte Welschinger den absolutte verdien av mengden
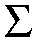s(C),
summen over alle reelle rasjonelle kurver C av grad d som interpolerer poengene. Han viste at denne vektede summen ikke avhenger av valg av poeng. Skriv Wd for denne invarianten av Welschinger. For eksempel så vi nettopp det W3=8.
Dette var et gjennombrudd, da Wd (nesten) var den første virkelig ikke-trivielle invarianten i enumerativ ekte algebraisk geometri. Noter det Wd er en nedre grense for antall reelle rasjonelle kurver gjennom 3d-1 virkelige poeng i flyet, og Wd\leq Nd.
Mikhalkin, som var arrangør av semesteret, ga nøkkelen til databehandling Wd ved hjelp av tropisk algebraisk geometri [Mi]. Dette er geometrien til den tropiske semiring, der operasjonene til maks og + på reelle tall erstatter de vanlige operasjonene av + og multiplikasjon. Et tropisk polynom er en stykkevis lineær funksjon av formen
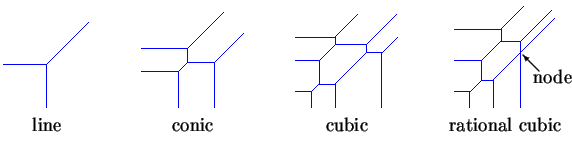
Graden av en tropisk kurve er antall stråler som har en tendens til uendelig i en av de tre retningene vest, sør eller nord øst. En tropisk kurve er rasjonell hvis det er en stykkevis lineær neddykking av et tre. Noder har valens 4.
Mikhalkin viste at det bare er endelig mange rasjonelle tropiske kurver av grad d som interpolerer 3d-1 generiske poeng. Mens antallet slike kurver avhenger av valg av punkter, festet Mikhalkin positive mangfoldigheter til hver tropiske kurve slik at den veide summen ikke blir, og faktisk er lik Nd. Han reduserte også disse mangfoldighetene og oppregningen av tropiske kurver til kombinatorikken av gitterbaner i en trekant med sidelengde d.
Mikhalkin brukte en korrespondanse som involverte kartet Log 🙁C*)2 –> R2 definert av (x,y)|–>(log|x|,log|y|), og en viss “stor kompleks grense” på den komplekse strukturen på (C*)2. Under denne store komplekse grensen deformeres rasjonelle kurver av grad d som interpolerer 3d-1 poeng i (C*)2 til “komplekse tropiske kurver”, hvis bilder under Log er vanlige tropiske kurver som interpolerer bildene av punktene. Multiplikasjonen av en tropisk kurve T er antall komplekse tropiske kurver som projiserer til T.
Hva med virkelige kurver? Etter denne korrespondansen festet Mikhalkin en reell mangfoldighet til hver tropiske kurve og viste at hvis de tropiske kurvene interpolerer en gitt 3d-1 poeng har total reell mangfoldighet N, så er det det 3d-1 reelle poeng som er interpolert av N reelle rasjonelle gradskurver d. Denne reelle mangfoldigheten kommer igjen til uttrykk i form av gitterbaner.
Hva med Welschingers invariant? På samme måte festet Mikhalkin en signert vekt på hver tropiske kurve (en tropisk versjon av Welschingers tegn) og viste at den tilsvarende vektede sum tilsvarer Welschingers invariant. Som tidligere kan denne tropiske signerte vekten uttrykkes i form av gitterbaner.
I løpet av semesteret ved MSRI brukte Itenberg, Kharlamov og Shustin [IKS] Mikhalkins resultater for å estimere Welschingers invariant. Det viste de Wd\geq d!/3, og også
Det er to andre tilfeller av dette fenomenet med lavere grenser, hvorav det første går foran Welschinger sitt arbeid. Anta at d er jevn og la W(s) være en skikkelig polynom av grad k(d–k+1). Så Eremenko og Gabrielov [EG] viste at det eksisterer virkelige polynomer f1(s),…, fk(s) av grad d hvis Wronski-determinant er W(s). Faktisk beviste de en nedre grense for antall k-tuple av polynomer, opp til en ekvivalens. Tilsvarende, mens jeg er hos MSRI, Soprunova og jeg [SS] studerte sparsomme polynomiske systemer assosiert med poseter, og viser at antallet virkelige løsninger er avgrenset nedenfor av tegn-ubalansen til posetten. Slike lavere grenser for tallrike problemer, som innebærer eksistensen av reelle løsninger, er viktige for applikasjoner.
For eksempel ble denne historien fortelles om øl en kveld på MSRI verksted på geometrisk modellering og ekte algebraisk geometri i april 2004. En deltaker, Schicho, innså at resultatet W3=8 for kubikk forklarte hvorfor en metode han hadde utviklet alltid så ut til å virke. Dette var en algoritme for å beregne en omtrentlig parametrisering av en bue av en kurve, via en reell rasjonell kubikk som interpolerer 8 punkter på buen. Det gjensto å finne forhold som garanterte eksistensen av en løsning som ligger nær buen. Dette ble nettopp løst av Fiedler-Le Touzé, en MSRI-postdoktor som hadde studert kubikk (ikke nødvendigvis rasjonell) og interpolert 8 poeng for å klassifisere reelle plankurver i grad 9.
Bibliografi
| [DK] | A. I. Degtyarev and V. M. Kharlamov, Topological properties of real algebraic varieties: Rokhlin’s way, Uspekhi Mat. Nauk 55 (2000), no. 4(334), 129–212. |
| [EG] | A. Eremenko and A. Gabrielov, Degrees of real Wronski maps, Discrete Comput. Geom. 28 (2002), no. 3, 331–347. |
| [IKS] | I. Itenberg, V. Kharlamov, and E. Shustin, Logarithmic equivalence of Welschinger and Gromov-Witten invariants, arXiv:math.AG/0407188. |
| [KM] | M. Kontsevich and Yu. Manin, Gromov-Witten classes, quantum cohomology, and enumerative geometry, Comm. Math. Phys. 164 (1994), no. 3, 525–562. |
| [Mi] | G. Mikhalkin, Enumerative tropical algebraic geometry in R2, arXiv:math.AG/0312530. |
| [SS] | E. Soprunova and F. Sottile, Lower Bounds for Real Solutions to Sparse Polynomial Systems, arXiv:math.AG/0409504. |
| [So] | F. Sottile, Enumerative real algebraic geometry, Algorithmic and quantitative real algebraic geometry (Piscataway, NJ, 2001), DIMACS Ser. Discrete Math. Theoret. Comput. Sci., vol. 60, Amer. Math. Soc., Providence, RI, 2003, pp. 139–179. |
| [W] | J.-Y. Welschinger, Invariants of real rational symplectic 4-manifolds and lower bounds in real enumerative geometry, C. R. Math. Acad. Sci. Paris 336 (2003), no. 4, 341–344. |
| [Ze] | H. G. Zeuthen, Almindelige Egenskaber ved Systemer af plane Kurver, Danske Videnskabernes Selskabs Skrifter, Naturvidenskabelig og Mathematisk, Afd. 10 Bd. IV (1873), 286–393. |
Vi takker takknemlig redaktøren vår, Silvio Levy og MSRI-medlemmene hvis arbeid vi beskriver.
Støttet av Nasjonal vitenskapelig stiftelse tilskudd CAREER DMS-0134860 og DMS-9810361 (finansiering av MSRI), og Clay matematisk institutt.
Sist endret: Mandag 23. april 15:33:30 CEST 2018