Original English version: http://galileoandeinstein.physics.virginia.edu/lectures/gkastr1.html
Michael Fowler UVa Fysikk Avdeling
I dette foredraget skal vi vise hvordan grekerne gjorde de første virkelige målinger av astronomiske avstander: Jordens størrelse og avstanden til månen, begge bestemt ganske nøyaktig, og avstanden til solen, hvor deres beste estimat falt kort av en faktor på to.
Hvor stor er Jorden?
Den første rimelig god måling av jordens størrelse ble gjort av Eratosthenes, en greker som levde i Alexandria, Egypt, i det tredje århundre f.Kr. Han visste at det var langt i sør, i byen Syene (dagens Aswan, der det nå er en stor damm på Nilen), og det var en dyp brønn og ved middagstid den 21. juni reflekterte sollyset fra vannet ned i denne brønnen, noe som skjedde på ingen annen dag i året. Poenget var at solen var akkurat vertikalt overhead på den tiden, og på ingen annen tid i året. Eratosthenes visste også at solen aldri var vertikalt overhead i Alexandria, nærmest den var den 21 juni, da den var av med en vinkel, viste han seg å være om lag 7,2 grader ved å måle skyggen av en vertikal pinne.
Avstanden fra Alexandria til Syene ble målt på 5.000 stades (en stade som var 500 fot), nesten helt rett sør. Fra dette, og forskjellen i sollysvinkelen ved middagstid 21. juni, var Eratosthenes i stand til å finne ut hvor langt det ville være å gå helt rundt jorden.
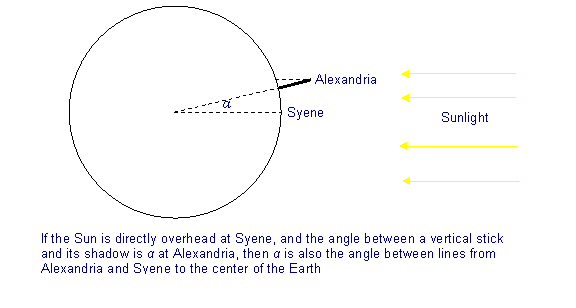
Selvfølgelig anerkjente Eratosthenes at jorda er sfærisk i form, og at “vertikalt nedover” hvor som helst på overflaten bare betyr retningen mot senteret fra det punktet. Dermed var to vertikale pinner, en i Alexandria og en i Syene, ikke egentlig parallelle. På den annen side var strålene av sollys fallende på de to sidene parallelle. Derfor, hvis solens stråler var parallelle med en vertikal pinne i Syene (så den ikke hadde skygge), var vinkelen de gjorde med staven i Alexandria den samme som hvor langt rundt i jorden, i grader, var Alexandria fra Syene.
Ifølge den greske historikeren Cleomedes, måler Eratosthenes vinkelen mellom sollys og pinne ved middagstid i midsommeren i Alexandria for å være 7,2 grader, eller en femtedel av en fullstendig sirkel. Det er tydelig at du tegner et bilde av dette at dette er samme vinkel som det mellom Alexandria og Syene sett fra sentrum av jorden, så avstanden mellom dem, de 5000 stadene, må være en femtedel av avstanden rundt jord, som derfor er lik 250.000 stad, ca 23.300 mil. Det riktige svaret er omtrent 25.000 miles, og faktisk har Eratosthenes vært nærmere enn vi har sagt her – vi er ikke helt sikre på hvor langt en stade var, og noen lærde hevder at det var omtrent 520 fot, noe som ville sette ham enda nærmere.
Hvor høy er månen?
Hvordan begynner vi å måle avstanden fra jorden til månen? En åpenbar tanke er å måle vinkelen til månen fra to byer langt fra hverandre samtidig, og konstruere en lignende trekant, som Thales måler avstanden til skipet til sjøs. Dessverre var vinkeldifferansen fra to punkter et par hundre miles fra hverandre for liten til å kunne måles av de teknikkene som var i bruk på den tiden, slik at metoden ikke ville fungere.
Likevel greske astronomer, som begynner med Aristarkhos (310-230 f.Kr., omtrent) kom opp med en smart metode for å finne månens avstand, etter nøye observasjon av en måneformørkelse, som skjer når jorden beskytter månen fra solens lys.
For en kort film som illustrerer en måneformørkelse, klikk her!
For bedre å visualisere en måneformørkelse, tenk å holde opp en fjerdedel (diameter en tomme ca.) på avstand der det bare blokkerer ut solens stråler fra det ene øyet. Selvfølgelig bør du ikke prøve dette-vil skade øyet! Du kan prøve det med fullmåne, som skjer for å være den samme synlige størrelsen på himmelen som solen. Det viser seg at riktig avstand er ca ni meters avstand, eller 108 inches. Hvis kvartalet er lenger unna enn det, er det ikke stor nok til å blokkere ut alle sollys. Hvis det er nærmere enn 108 inches, vil det fullstendig blokkere sollys fra noen små sirkulært område, som gradvis øker i størrelse beveger seg mot kvartal. Dermed den delen av plassen der sollyset er helt blokkert er konisk, som en lang langsomt avsmalnende iskrem kjegle, med punktet 108 inches bak kvartal. Selvfølgelig er dette omgitt av et uklart område, kalt “penumbra”, der sollyset er delvis blokkert. Den fullt skraverte området kalles “umbra”. (Dette er latin for skygge. Umbrella betyr lite skygge på italiensk.) Hvis du tape en kvart på slutten av en tynn pinne, og hold den i solen på riktig måte, kan du se disse ulike skyggeområder.
Spørsmål: Hvis du har brukt en krone i stedet for et kvartal, hvor langt fra øyet ditt vil du måtte holde den å bare blokkere hele måneskinn fra det øyet? Hvordan de ulike avstander forholder seg til de relative størrelser av krone og kvartal? Tegn et diagram som viser de to koniske skygger.
Nå forestille du er ute i verdensrommet, litt avstand fra jorden, ser på jordens skygge. (Selvfølgelig kan du bare virkelig se den hvis du skutt ut en sky av ørsmå partikler og så hvem av dem som glinset i sollyset, og som var i mørket.) Det er tydelig må jordens skygge være konisk, akkurat som det fra kvartalet. Og det må også være lik for kvartalet i teknisk forstand-det må være 108 jord diametre lang! Det er fordi kjeglens spiss er lengst punkt ved hvilket jorden kan blokkere alle sollys, og forholdet mellom den avstand til diameteren blir bestemt av vinkelstørrelsen av solen blir blokkert. Dette betyr at membranen er 108 jord diametre lang og langt punktet 864,000 miles fra jorden.
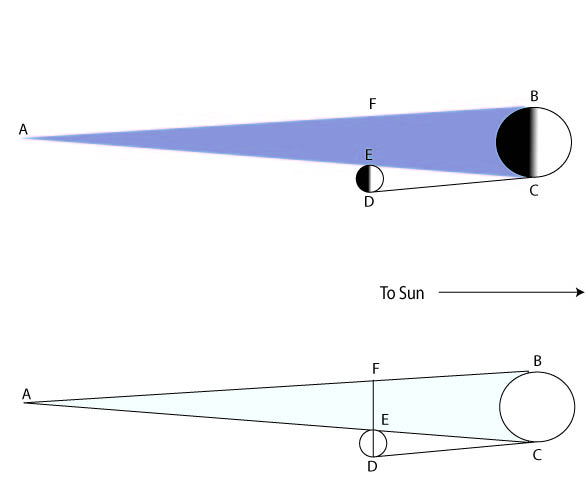
Nå, i løpet av en total måne formørkelse månen beveger seg inn i denne kjegle av mørket. Selv når månen er helt inne i skyggen, det kan fortsatt bli svakt sett, på grunn av lys spredt av jordens atmosfære. Ved å observere månen nøye under formørkelsen, og se hvordan jordens skygge falt på det, grekerne fant ut at diameteren av jordens konisk skygge på avstanden til månen var ca to og en halv ganger månens egen diameter.
Merk: Det er mulig å sjekke dette estimatet, enten fra et fotografi av månen som kommer inn i jordens skygge, eller, bedre, ved faktisk observasjon av en måneformørkelse.
Spørsmål: På dette tidspunkt kjente grekerne jordens størrelse (omtrent en sfære 8000 mil i diameter) og derfor størrelsen på jordens koniske skygge (lengde 108 ganger 8000 mil). De visste at når månen passerte gjennom skyggen, var skyggen diameter på den avstanden to og en halv ganger månens diameter. Var det nok informasjon å finne ut hvor langt var månen?
Vel, det gjorde fortelle dem månen var ikke lenger unna enn 108 × 8000 = 864000 miles, ellers månen ikke ville passere gjennom jordens skygge i det hele tatt! Men ut fra det vi har sagt så langt, kan det være en liten måne nesten 864 000 miles away, passerer gjennom den siste bit av skyggen nær punktet. Men en slik liten måne aldri kunne føre til en solar eclipse. Faktisk, som grekerne visste godt, er månen den samme synlige størrelsen på himmelen som solen. Dette er avgjørende ekstra faktum de pleide å spikre ned månens avstand fra jorden.
De løste problemet ved hjelp av geometri, konstruerer figuren nedenfor. I denne figuren betyr at det faktum at månen og solen har samme tilsynelatende størrelse på himmelen, betyr at vinkelen ECD er den samme som vinkelen EAF. Legg merke til at lengden FE er diameteren til jordens skygge på månens avstand, og lengden ED er månens diameter. Grekerne fant ved observasjon av månens formørkelse at forholdet mellom FE og ED var 2,5 til 1, og så på liknende isosceles triangler FAE og DCE, utledes vi at AE er 2,5 ganger så lang som EC, hvorav AC er 3,5 ganger så lenge som EC. Men de visste at AC må være 108 jorddiameter i lengde, og å ta jordens diameter til 8000 miles, er det lengste punktet av den koniske skyggen, A, 864.000 miles fra jorden. Fra det ovennevnte argumentet er dette 3,5 ganger lenger unna enn månen er, så avstanden til månen er 864 000, ca. 240 000 miles. Dette er innen noen få prosent av riktig tall. Den største feilkilden er sannsynligvis estimatet av forholdet mellom månens størrelse og jordens skygge når det går gjennom.
Hvor langt unna er solen?
Dette var et enda vanskeligere spørsmål de greske astronomene spurte seg selv, og de gjorde det ikke så bra. De kom opp med en veldig genial metode for å måle solens avstand, men det viste seg for krevende fordi de ikke kunne måle den viktige vinkelen nøyaktig nok. Likevel lærte de fra denne tilnærmingen at solen var langt lenger unna enn månen, og følgelig, siden den har samme tilsynelatende størrelse, må den være mye større enn enten månen eller jorden.
Ideen til å måle solens avstand var veldig enkelt i prinsippet. De visste selvfølgelig at månen skinnet ved å reflektere solens lys. Derfor rangerte de, når månen ser ut til å være akkurat halvfull, må linjen fra månen til solen være nøyaktig vinkelrett på linjen fra månen til observatøren (se figuren for å overbevise deg selv om dette). Så hvis en observatør på jorden, ved å observere en halvmåne i dagslys, måler nøye vinkelen mellom månens retning og solens retning, vinkelen a i figuren, skal han kunne bygge en lang, tynn trekant , med sin grunnlinje jordmånelinjen, med en vinkel på 90 grader i den ene enden og den ene, og så finner du forholdet mellom solens avstand til månens avstand.
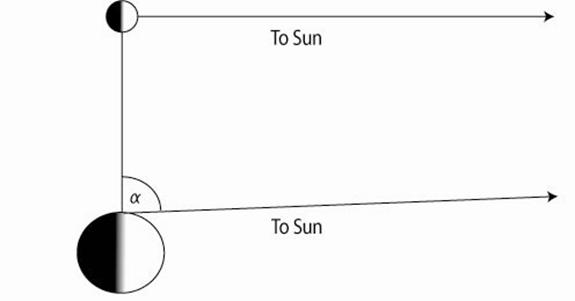
Problemet med denne løsning er at vinkelen a viser seg å være forskjellig fra 90 grader med omtrent en sjettedel av en grad, for liten til å måle nøyaktig. Det første forsøket var Aristarkus, som anslås vinkelen å være 3 grader. Dette ville sette solen bare fem million miles away. Men det ville allerede foreslå solen for å være mye større enn jorden. Det var trolig denne erkjennelsen som førte Aristarkus å foreslå at solen, snarere enn jorden, var i sentrum av universet. De beste senere greske forsøk funnet solens avstand til å være omtrent halvparten riktig verdi (92 millioner miles).
Presentasjonen her er lik som i Eric Rogers, fysikk for den spørrende sinn, Princeton, 1960.
